统计学在期权定价和交易中的应用(2)

　　etf50[ 'rea_var'] = 252* np.cumsum(etf50[ 'returns'] ** 2) / np.arange(len(etf50))etf50[ 'rea_vol'] = np.sqrt(etf50[ 'rea_var'])print_statistics(etf50)

RETURN SAMPLE STATISTICS

---------------------------------------------

Mean of Daily Log Returns -0.000067

Std of Daily Log Returns 0.021153

Mean of Annua. Log Returns -0.016917

Std of Annua. Log Returns 0.335787

---------------------------------------------

Skew of Sample Log Returns -0.734791

Skew Normal Test p-value 0.000000

---------------------------------------------

Kurt of Sample Log Returns 4.597651

Kurt Normal Test p-value 0.000000

---------------------------------------------

Normal Test p-value 0.000000

---------------------------------------------

Realized Volatility 0.335789

Realized Variance 0.112754

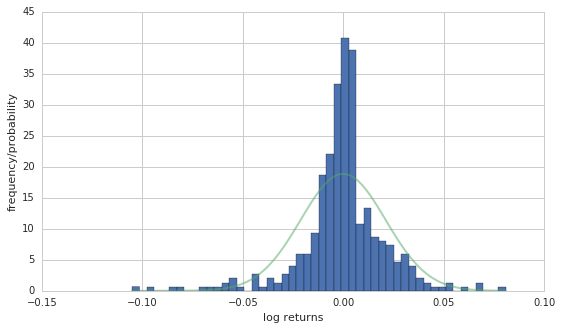
　　# histogram of annualized daily log returns

　　defreturn_histogram(data):''' Plots a histogram of the returns. '''plt.figure(figsize=( 9, 5)) x = np.linspace(min(data[ 'returns'][ 1:]), max(data[ 'returns'][ 1:]), 100) plt.hist(np.array(data[ 'returns'][ 1:]), bins= 50, normed= True) y = dN1(x, np.mean(data[ 'returns'][ 1:]), np.std(data[ 'returns'][ 1:])) plt.plot(x, y, linewidth= 2) plt.xlabel( 'log returns') plt.ylabel( 'frequency/probability') plt.grid( True)return_histogram(etf50)

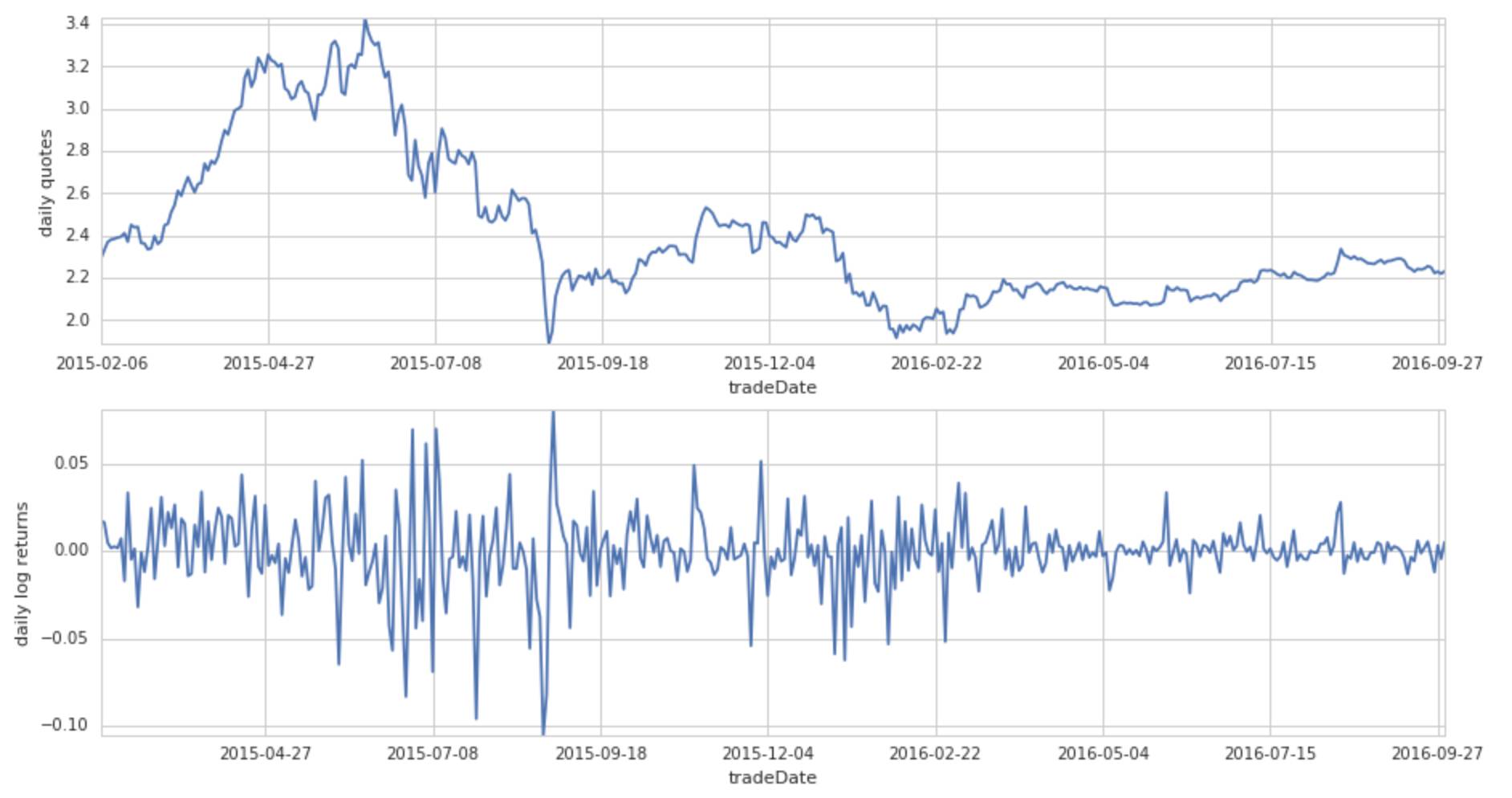
　　etf50.index = etf50[ 'tradeDate']quotes_returns(etf50)

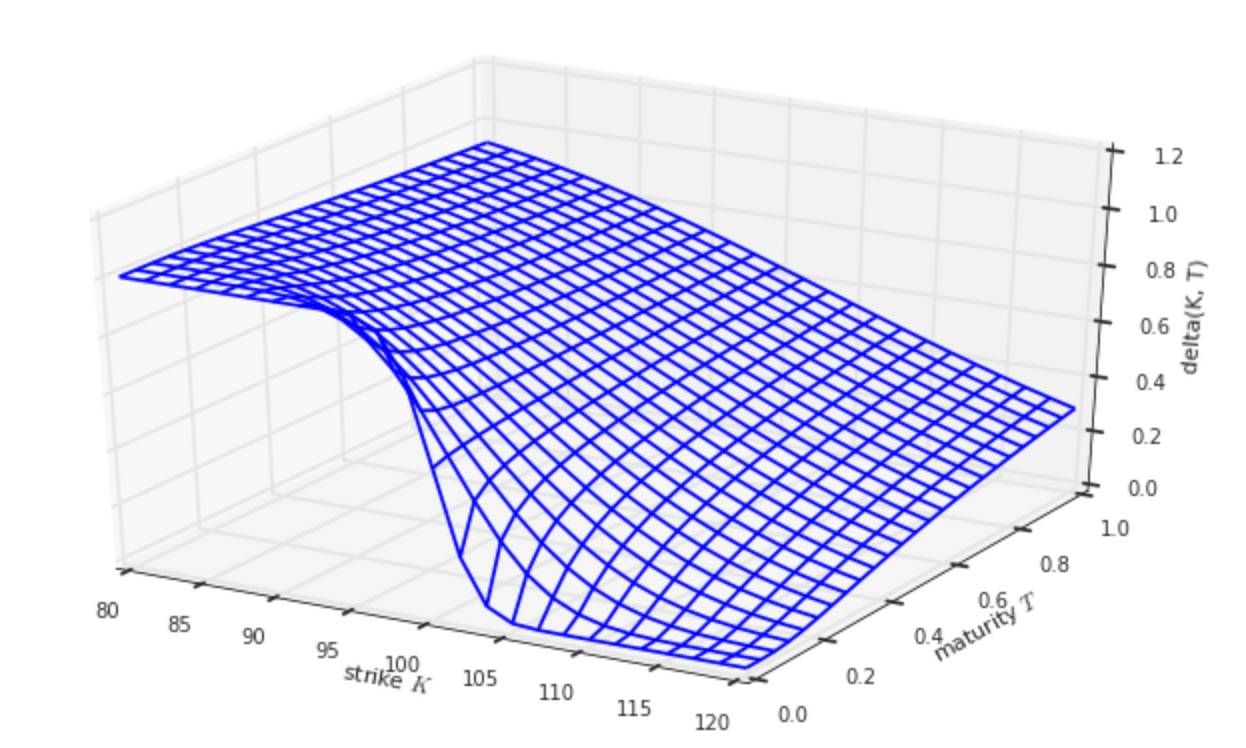
　　期权的Greeks

期权的Greeks主要描述了期权价格对其标的的资产价格、到期时间、波动率和无风险利率四个参数值的敏感性指标。

　　plot_greeks(BSM_delta, 'delta')

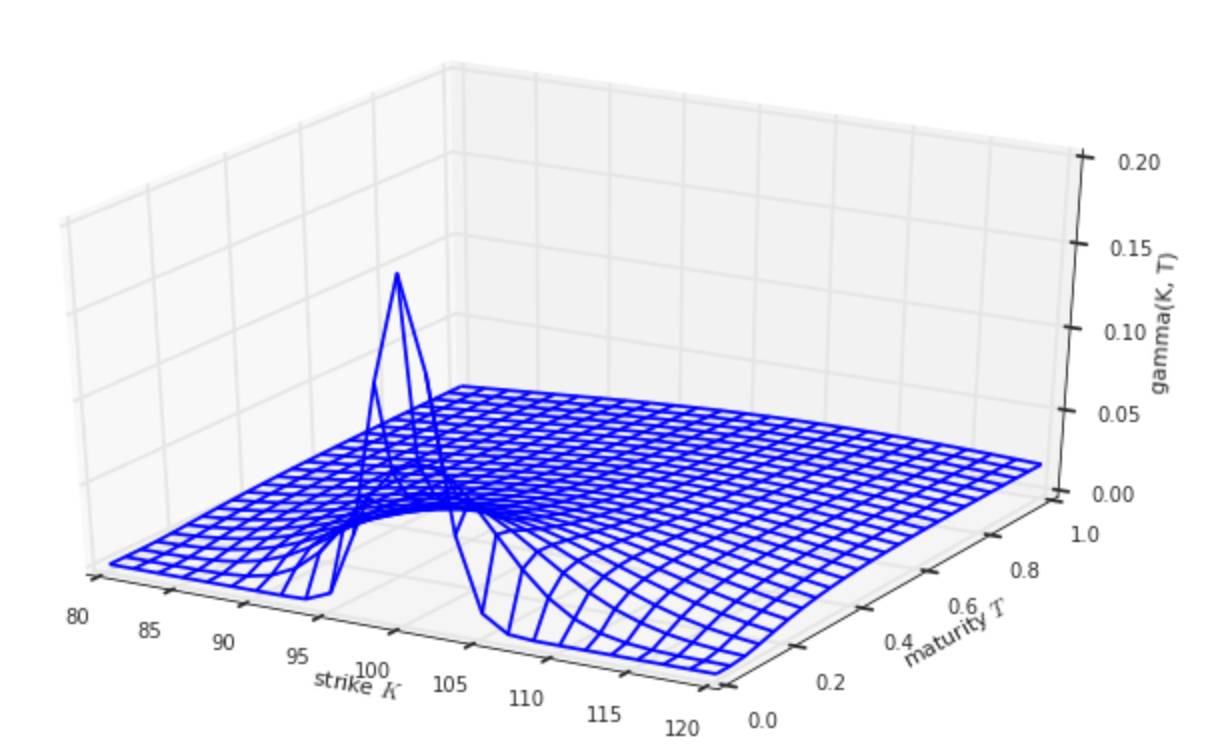
　　plot_greeks(BSM_gamma, 'gamma')

　　plot_greeks(BSM_theta, 'theta')

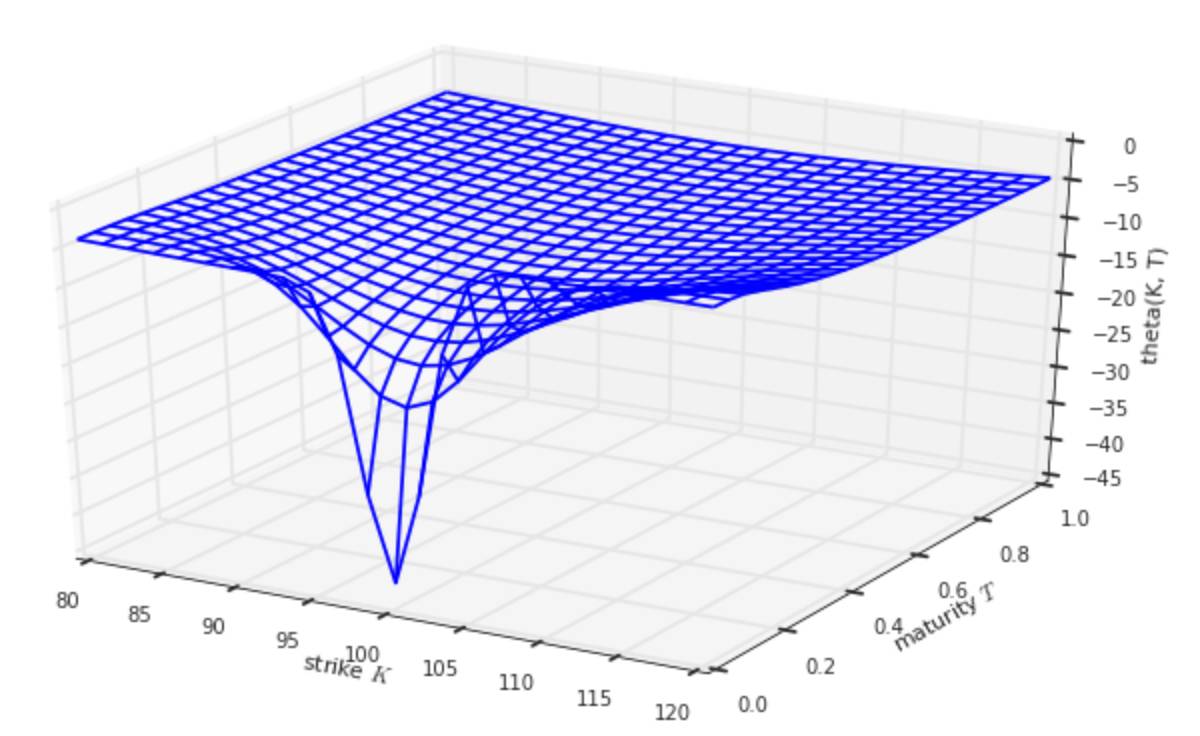
　　plot_greeks(BSM_rho, 'rho')

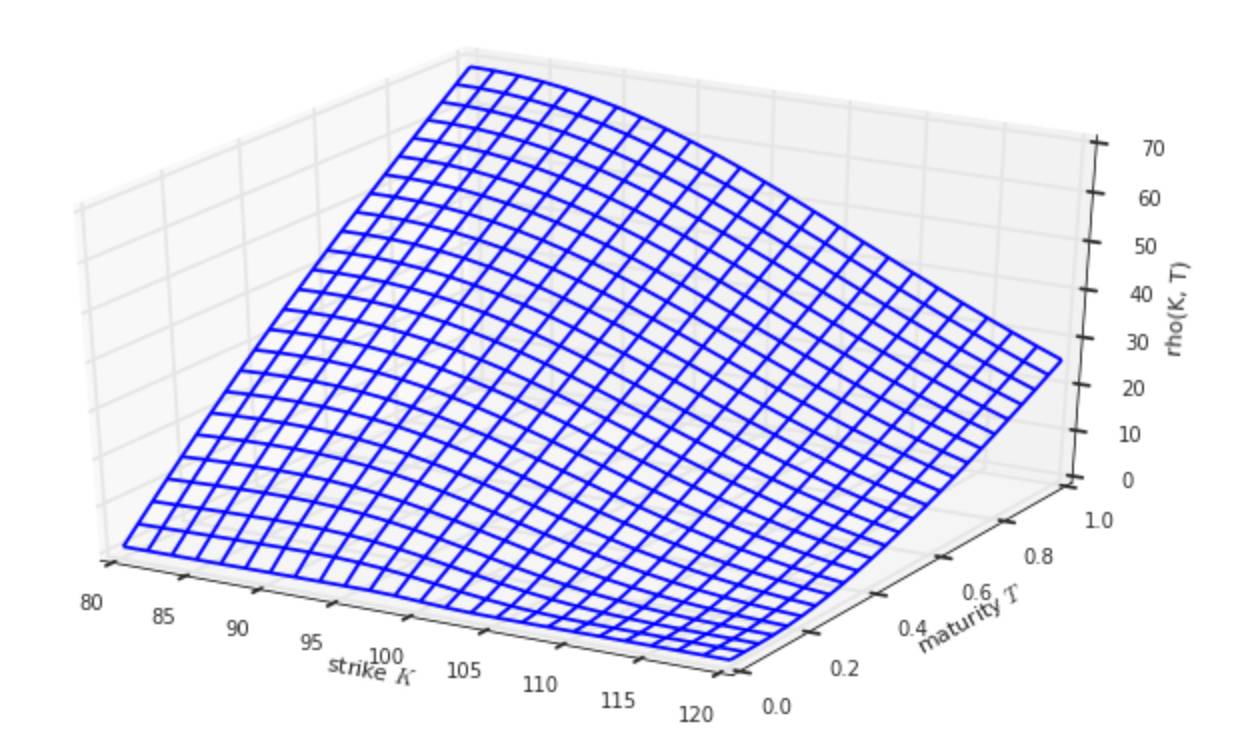
　　plot_greeks(BSM_vega, 'vega')

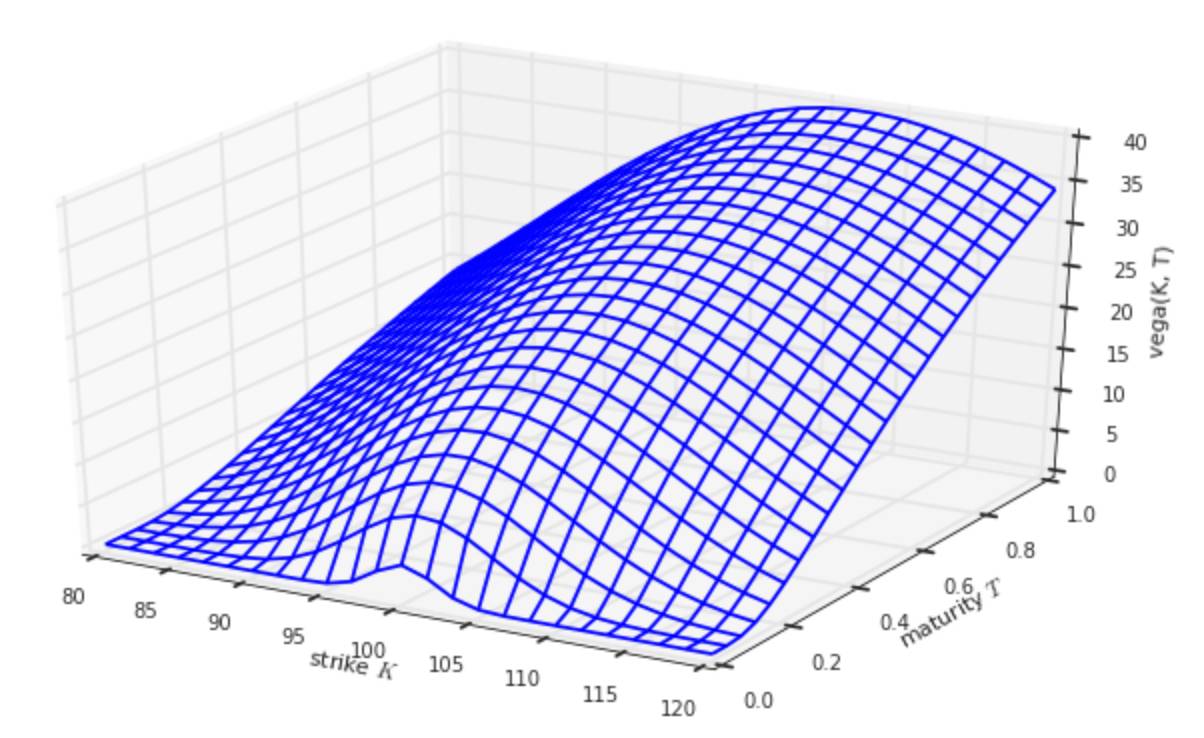
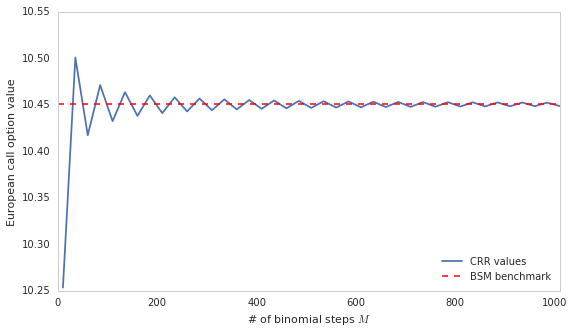
　　二叉树模型和BSW模型

　　BSM_benchmark = BSM_call_value(S0, K, 0, T, r, sigma)BSM_benchmark

　　10.45058357218553

　　CRR_option_value(S0, K, T, r, sigma, 'call', M= 2000)

　　10.449583775457942

　　plot_convergence( 10, 1011, 20)

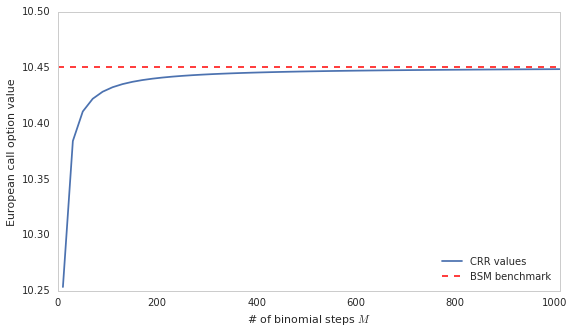
　　plot_convergence( 10, 1011, 25)

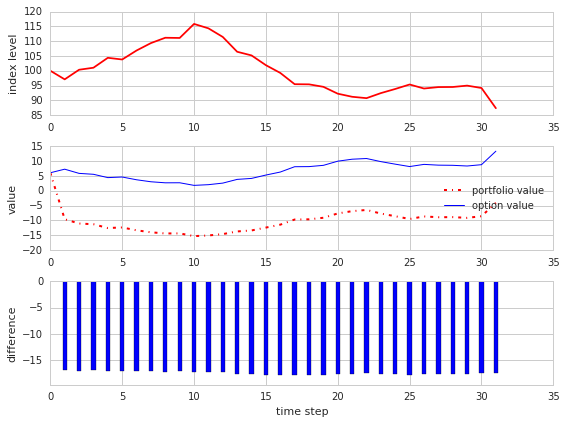
　　动态对冲

　　S, po, vt, errs, t = BSM_hedge_run(p= 25)

　　APPROXIMATION OF FIRST ORDER ----------------------------- step | S_t | Delta 1 | 97.10 | -0.46 2 | 100.34 | -0.40 3 | 101.03 | -0.39 4 | 104.38 | -0.30 5 | 103.81 | -0.32 6 | 106.85 | -0.27 7 | 109.36 | -0.22 8 | 111.16 | -0.21 9 | 111.09 | -0.20 wrong 10 | 115.83 | -0.15

　　（部分）

　　plot_hedge_path(S, po, vt, errs, t)

　　pl_list = BSM_dynamic_hedge_mcs(M= 200, I= 150000)

　　Value of American Put Option is 4.461

　　Delta t=0 is -0.011

　　run 1000 p/l 0.044

　　run 2000 p/l 0.042

　　run 3000 p/l 0.305

　　run 4000 p/l 0.969

　　run 5000 p/l -0.330

　　run 6000 p/l 0.093

　　run 7000 p/l -0.438

　　run 8000 p/l -0.156

　　run 9000 p/l -0.126

　　run 10000 p/l 0.187

　　SUMMARY STATISTICS FOR P&L

　　---------------------------------

　　Dynamic Replications 10000

　　Time Steps 200

　　Paths for Valuation 150000

　　Maximum 2.358

　　Average 0.008

　　Median 0.006

　　Minimum -1.641