统计学在期权定价和交易中的应用
2017-05-19 编辑:
编辑部
微信公众号
关键字全网搜索最新排名
『量化投资』:排名第一
『量 化』:排名第一
『机器学习』:排名第四
我们会再接再厉
成为全网优质的金融、技术类公众号
公众号与优矿联合推出几期关于期权知识的分享。希望能给大家从不同角度解读期权知识。
期权定价与内在价值
常见的期权内在价值被定义为0与期权立刻执行所能获得回报的较大值,即max(S-K, 0)(看涨期权的情形)和max(K-S, 0)(看跌期权的情形)。
# Option Strike
K = 8000
# Graphical Output
S = np.linspace( 7000, 9000, 100) # index level values
h = np.maximum(S - K, 0) # inner values of call option
plt.figure()plt.plot(S, h, lw= 2.5) # plot inner values at maturity
plt.xlabel( 'index level $S_t$ at maturity')plt.ylabel( 'inner value of European call option')plt.grid( True)
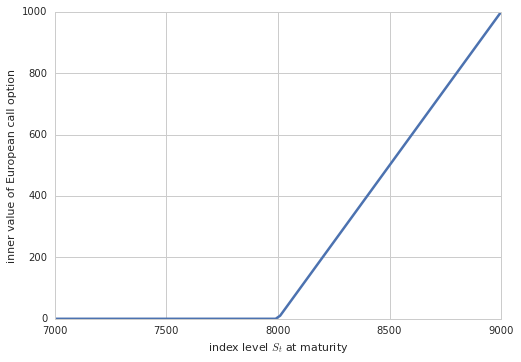
下面的代码是使用BSM模型来对期权进行定价:
无收益资产欧式看涨期权的定价公式:
无收益资产欧式看跌期权的定价公式:
下面画出了根据BSM模型计算出的期权的现值
# Model and Option Parameters
K = 8000# strike price
T = 1.0# time-to-maturity
r = 0.025# constant, risk-less short rate
vol = 0.2# constant volatility
# Sample Data Generation
S = np.linspace( 4000, 12000, 150) # vector of index level values
h = np.maximum(S - K, 0) # inner value of option
C = [BSM_call_value(S0, K, 0, T, r, vol) forS0 inS] # calculate call option values# Graphical Output
plt.figure()plt.plot(S, h, 'g-.', lw= 2.5, label= 'inner value') # plot inner value at maturity
plt.plot(S, C, 'r', lw= 2.5, label= 'present value')
# plot option present valueplt.grid( True)plt.legend(loc= 0)plt.xlabel( 'index level $S_0$')plt.ylabel( 'present value $C(t=0)$')
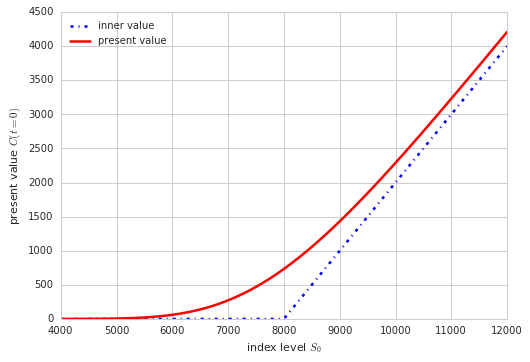
历史波动率刻画
已经知道,B-S-M期权定价公式中的期权价格取决于下列五个参数:标的资产的市场价格,执行价格,到期期限,无风险利率和标的资产价格波动率。这五个参数中,前三个都是交易获得确定的值,在发达的经济市场,无风险利率也很容易估计,而估计标的资产的波动率要比估计无风险利率要困难的多。估计标的资长价格波动率有两种方法:历史波动率和隐含波动率。
所谓历史波动率,就是从标的资产价格的历史数据中计算出价格对数收益率的标准差,具体方法一般有以下两种:
直接估计(矩估计)
GARCH模型
很遗憾,GARCH模型在中国市场无效。
模拟数据
gbm = simulate_gbm()print_statistics(gbm)
RETURN SAMPLE STATISTICS
---------------------------------------------
Mean of Daily Log Returns 0.000294
Std of Daily Log Returns 0.012479
Mean of Annua. Log Returns 0.074109
Std of Annua. Log Returns 0.198092
---------------------------------------------
Skew of Sample Log Returns 0.008369
Skew Normal Test p-value 0.861095
---------------------------------------------
Kurt of Sample Log Returns 0.059948
Kurt Normal Test p-value 0.495981
---------------------------------------------
Normal Test p-value 0.781084
---------------------------------------------
Realized Volatility 0.198147
Realized Variance 0.039262
quotes_returns(gbm)
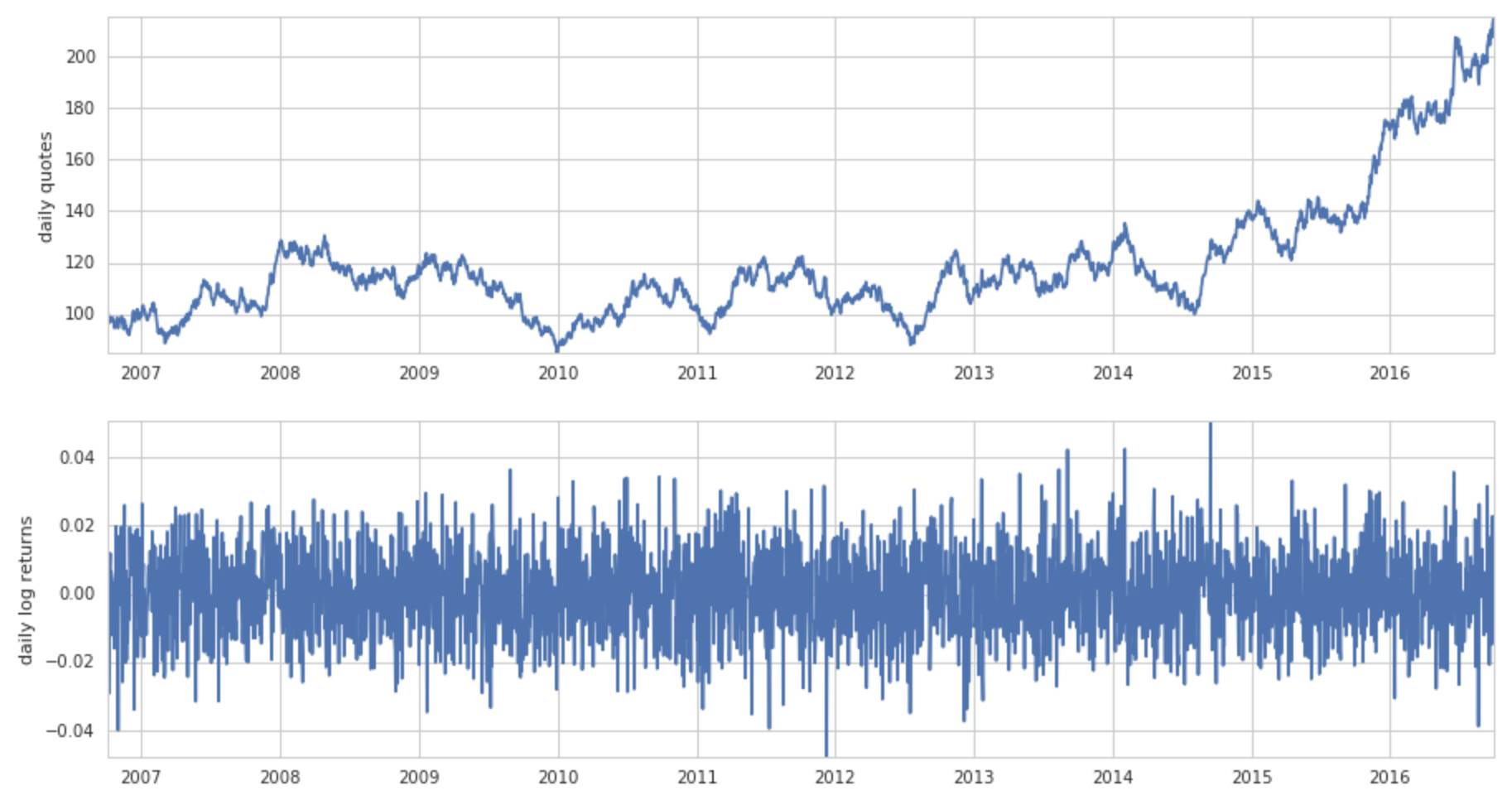
上证50ETF的实际波动率
etf50 = DataAPI.MktFunddGet(ticker= u"510050",beginDate= u"20150206",endDate= u"20160929",field=[ u"closePrice", u"tradeDate"] ,pandas= "1")etf50.set_index=( "tradeDate")etf50[ 'returns'] = np.log(etf50[ 'closePrice'] /etf50[ 'closePrice'].shift( 1))
# Realized Volatility (eg. as defined for variance swaps)