腾讯QQ社交网络的四度分离
2017-05-23 编辑:
作者 | 黄俊
责编 | 郭芮
在社会学领域有一个六度分离理论,认为任意两个人平均只需通过 6 个中间人就能找到对方。最初这个结论来自数百名志愿者组成的社会学实验,后来微软和Facebook 相继利用大量线上用户测量了更准确的值。而现在,我们在 QQ 这一中国人使用最广泛的社交网络上,实现了千亿关系链的社交距离计算,发现平均意义下任意两个QQ 用户只需要 4.20 个中间人的介绍就能够找到对方,即 QQ 社交网络的四度分离。
六度分离的前世今生
1929 年匈牙利作家考林西(Frigyes Karinthy)[1]在他的短篇作品《枷锁(Chains)》里面,猜想随着交通和信息传播技术的进步,社会结构会逐渐“缩小”,使得人与人的联系会更加紧密。在故事中他提出了一个假设:两个完全陌生的人可以通过不超过五个人产生联系。他认为世界虽大,但人们建立联系的代价可能比预想的要小。
为了验证这个猜想,1967年哈佛大学的一位社会科学家斯坦利?米拉尔格姆(Stanley Milgram)做了一个实验[2],他随机选 296 个志愿者[3],要求他们转发一个信件给一位他们不认识的住在波士顿的经纪人。为了能够让信件送到,斯坦利让他们把信件转给最有可能认识这位经纪人的人,然后希望能够通过不断转递的形式让信件出现在这位经纪人的手上。在事后的统计中,斯坦利发现平均只需要5.7个中间人就能够让信件到达。根据这一结论,斯坦利提出了著名的“六度分离”假说。
随着科技的进步,研究者们发现在更大规模的社交网络上验证这一猜想变为可能。2006年微软的研究者[4]用了当年6月份的 MSN 消息,在1.8亿的用户中随机选了1000个用户,计算他们通过MSN的消息链条能够到达的每一个角落,发现平均来说任意两个人之间的距离只有6.6。也就是说中间只需要5.6个中间人介绍就能够让两个陌生人认识。这是首次在星球级别的网络上验证“六度分离理论”。
到了2011年,Facebook联合米兰大学研究了7.21亿活跃用户构建的好友网络,估计出了任意两个用户之间的距离分布,发现 Facebook 网络的平均距离只有4.74,代表只需要3.74个中间人就能够让人们相互认识,据此他们写出了名为“四度分离”的论文[5]。
QQ社交网络的小世界
作为中国最大的即时通讯服务提供商,QQ 社交网络覆盖了中国大部分上网人口,而 QQ 的社交网络数据对外界却显得非常神秘。作为一个关系型社会,中国网民之间的关系是否比海外网民的关系更加紧密?这里,我们基于海量的 QQ 关系链数据,通过一定的算法(文章第二部分会详细介绍),计算出来任意两个 QQ 用户的平均距离。
| 网络 | 用户数 | 网络密度[6] | 平均距离 |
|---|---|---|---|
| QQ [7] | 8.21亿 | 8.4E-08 | 5.20 |
| Facebook [8] | 7.21亿 | 26.4E-08 | 4.74 |
| MSN [9] | 1.80亿 | 8.3E-08 | 6.6 |
平均距离为5.20,意味着平均来说任意两个QQ用户只需要4.20个中间人的介绍,就能够找到对方,我们称为“腾讯QQ社交网络的四度分离”。用 2011 年的Facebook 社交网络以及当年的 MSN 数据作对比,我们发现如今的 QQ 活跃用户更多,但 Facebook 的网络密度更大(网络密度 = 关系链数 / (用户数*(用户数-1),越大说明网络越稠密)。或许这跟 Facebook 的开放性有关,在 Facebook 用户能够看到对方以及对方的好友列表,这样更容易通过好友形成关系链。这里可以看到的是,QQ 社交网络的网络密度只有Facebook 的 30%,但计算得到的平均距离只比Facebook 多0.46,也就是说,网络更加稠密,但是网络中人与人的平均距离并没有非常明显地下降。这反映了两个社交网络结构的不同之处,QQ社交网络能够用更低的关系链稠密度,保持社会信息同样高效的传播。
另外,这里的距离是平均的概念,也就是说并不是任意两个用户之间的距离都是5.20。具体的分布如下图1。
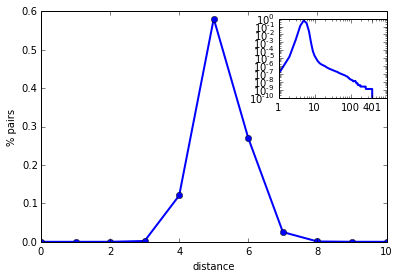
图1 任意两个用户的社交距离分布
图中横坐标是两个用户之间的距离,纵坐标是该距离的用户对占所有可达用户对[10]的比例。这里为了方便我们只画出了距离从 0 到 10 的部分。我们观察任意两个用户之间距离的分布,可以看出有接近60%用户对的最短距离都是5,实际上有 97% 的用户对距离都不超过6,所以严格意义上讲,平均来说一个用户通过不超过5次介绍就能够认识到 97% 的QQ用户。而这个分布的最大值其实是远大于5的。在我们的计算中距离最大的两个用户[11],他们的距离有401,则对于这两个人来说,需要400个中间人介绍才能够互相认识。而 Facebook 的网络只有 58。
海量关系链计算背后的技术
HyperANF 算法
而为了计算出QQ关系链的距离分布,我们采用了米兰大学 Web 实验室提出的的 HyperANF算法[12]。这个算法采用图计算经典的标签传播架构,其计算步骤如下:
初始化:每个节点存储一个“通讯录”,开始时只记录自己
迭代:当前次数 t
扩散:每个节点给邻居发送“通讯录”
聚合:每个节点把收到的“通讯录”,加上自己已有的做合并
统计:计算每个“通讯录”的大小,记为 B(t)
判断停止:如果 B(t) 相较上一轮计算出的 B(t-1)有增长,则继续迭代
结束:最后根据得到的序列 B(t),t=0,1,2……计算出平均距离
算法在第 t 轮迭代中,用户 x 的通讯录 B(x, t) 实际上记录的是自己所有距离不超过 t 的用户集合,因为有以下公式:
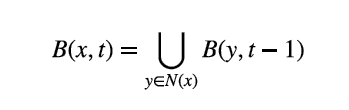
其中 N(x) 代表用户 x 的好友列表。距离用户 x 不超过 t 的用户集合等于自己所有好友的 “距离不超过 t-1 集合”的并集。
而如果我们把用户 x 在两次迭代的通讯录做差集,那我们就能够得到用户 x 距离恰好为 t 的用户列表。从而我们可以在算法的最后,得到任意距离为 t 的用户对数量。
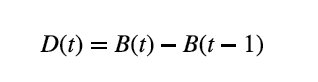
其中 D(t) 是网络中距离刚好为 t 的用户对数量,而
HyperLogLog 计数器
