回归、分类与聚类:三大方向剖解机器学习算法的优缺点(附Python和R实现)
2017-05-20 编辑:
选自EliteDataScience
机器之心编译
参与:蒋思源、晏奇
在本教程中,作者对现代机器学习算法进行一次简要的实战梳理。虽然类似的总结有很多,但是它们都没有真正解释清楚每个算法在实践中的好坏,而这正是本篇梳理希望完成的。因此本文力图基于实践中的经验,讨论每个算法的优缺点。而机器之心也在文末给出了这些算法的具体实现细节。
对机器学习算法进行分类不是一件容易的事情,总的来看,有如下几种方式:生成与判别、参数与非参数、监督与非监督等等。
然而,就实践经验来看,这些都不是实战过程中最有效的分类算法的方式。因为对于应用机器学习而言,开发者一般会在脑海中有一个最终目标,比如预测一个结果或是对你的观察进行分类。
因此,我们想介绍另一种对算法进行分类的路数,其基于机器学习任务来分类。
没有免费午餐定理
在机器学习中,有个定理被称为「没有免费的午餐」。简而言之,就是说没有一个算法可以完美解决所有问题,而且这对于监督学习(即对预测的建模)而言尤其如此。
举个例子,你不能说神经网络就一定任何时候都比决策树优秀,反过来也是。这其中存在很多影响因素,比如你数据集的规模和结构。

所以,当你使用一个固定的数据测试集来评估性能,挑选最适合算法时,你应该针对你的问题尝试多种不同的算法。
当然,你所使用的算法必须要适合于你试图解决的问题,这也就有了如何选择正确的机器学习任务这一问题。做个类比,如果你需要打扫你的房子,你可能会用吸尘器、扫帚或者是拖把,但是你绝不会掏出一把铲子然后开始挖地。
机器学习任务
在本次梳理中,我们将涵盖目前「三大」最常见机器学习任务:
回归方法
分类方法
聚类方法
说明:
本文的梳理不会涵盖具体领域的问题,比如自然语言处理。
本文也不会对每个算法都进行梳理。因为现有太多算法,而且新的算法也层出不穷。然而,这份清单将向读者展现对每个任务而言目前具有代表性的算法概览。
1、回归方法
回归方法是一种对数值型连续随机变量进行预测和建模的监督学习算法。使用案例一般包括房价预测、股票走势或测试成绩等连续变化的案例。
回归任务的特点是标注的数据集具有数值型的目标变量。也就是说,每一个观察样本都有一个数值型的标注真值以监督算法。
1.1 线性回归(正则化)
线性回归是处理回归任务最常用的算法之一。该算法的形式十分简单,它期望使用一个超平面拟合数据集(只有两个变量的时候就是一条直线)。如果数据集中的变量存在线性关系,那么其就能拟合地非常好。
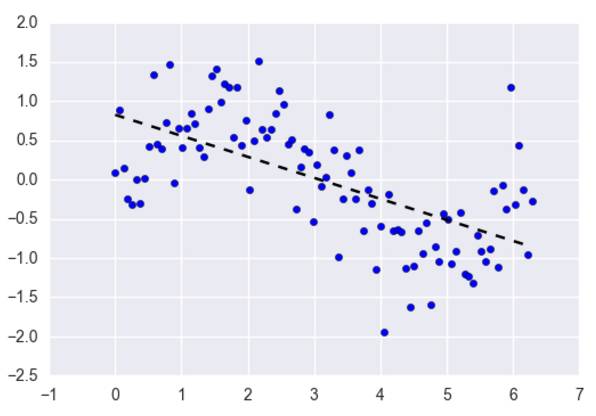
在实践中,简单的线性回归通常被使用正则化的回归方法(LASSO、Ridge 和 Elastic-Net)所代替。正则化其实就是一种对过多回归系数采取惩罚以减少过拟合风险的技术。当然,我们还得确定惩罚强度以让模型在欠拟合和过拟合之间达到平衡。
优点:线性回归的理解与解释都十分直观,并且还能通过正则化来降低过拟合的风险。另外,线性模型很容易使用随机梯度下降和新数据更新模型权重。
缺点:线性回归在变量是非线性关系的时候表现很差。并且其也不够灵活以捕捉更复杂的模式,添加正确的交互项或使用多项式很困难并需要大量时间。
Python 实现:http://scikit-learn.org/stable/modules/linear_model.html
R 实现:https://cran.r-project.org/web/packages/glmnet/index.html
1.2 回归树(集成方法)
回归树(决策树的一种)通过将数据集重复分割为不同的分支而实现分层学习,分割的标准是最大化每一次分离的信息增益。这种分支结构让回归树很自然地学习到非线性关系。
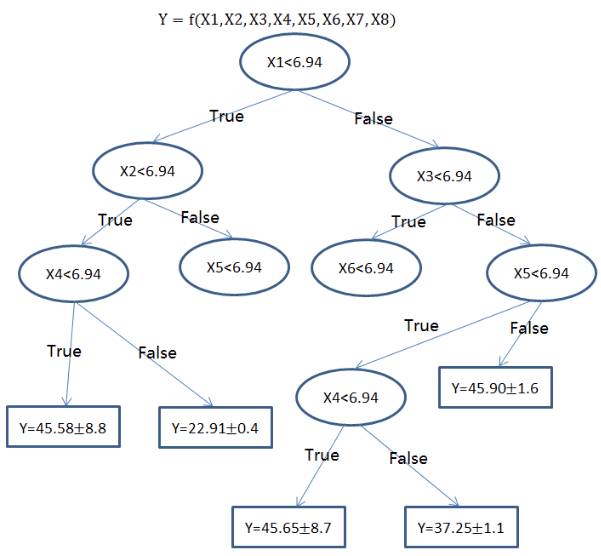
集成方法,如随机森林(RF)或梯度提升树(GBM)则组合了许多独立训练的树。这种算法的主要思想就是组合多个弱学习算法而成为一种强学习算法,不过这里并不会具体地展开。在实践中 RF 通常很容易有出色的表现,而 GBM 则更难调参,不过通常梯度提升树具有更高的性能上限。
优点:决策树能学习非线性关系,对异常值也具有很强的鲁棒性。集成学习在实践中表现非常好,其经常赢得许多经典的(非深度学习)机器学习竞赛。
缺点:无约束的,单棵树很容易过拟合,因为单棵树可以保留分支(不剪枝),并直到其记住了训练数据。集成方法可以削弱这一缺点的影响。
随机森林 Python 实现:http://scikit-learn.org/stable/modules/ensemble.html#random-forests
随机森林 R 实现:https://cran.r-project.org/web/packages/randomForest/index.html
梯度提升树 Python 实现:http://scikit-learn.org/stable/modules/ensemble.html#classification