seq2seq理论研究和在量化上的延伸系列一(思路+代码)(3)
2017-05-13 编辑:
batch_ = [[ 6], [ 3, 4], [ 9, 8, 7]]batch_, batch_length_ = helpers.batch(batch_)print( 'batch_encoded:n'+ str(batch_))din_, dlen_ = helpers.batch(np.ones(shape=( 3, 1), dtype=np.int32), max_sequence_length= 4)print( 'decoder inputs:n'+ str(din_))pred_ = sess.run(decoder_prediction, feed_dict={ encoder_inputs: batch_, decoder_inputs: din_, })print( 'decoder predictions:n'+ str(pred_))
batch_encoded:[[6 3 9] [0 4 8] [0 0 7]]decoder inputs:[[1 1 1] [0 0 0] [0 0 0] [0 0 0]]decoder predictions:[[9 3 9] [9 0 9] [0 0 0] [0 0 0]]
toy task
我们将教我们的模型记忆和再现输入序列。 序列将是随机的,具有不同的长度。
由于随机序列不包含任何结构,模型将无法利用数据中的任何模式。 它将简单地在思维向量中编码序列,然后从中解码。
batch_size = 100batches = helpers.random_sequences(length_from= 3, length_to= 8,vocab_lower= 2, vocab_upper= 10,batch_size=batch_size)print( 'head of the batch:')
forseq innext(batches)[: 10]: print(seq) head of the batch:[7, 2, 4, 5, 7, 6][5, 4, 8, 2, 9, 8, 2][3, 6, 9, 4, 4, 7][8, 8, 6, 7, 4][5, 8, 5, 9, 2, 8, 8, 5][9, 4, 6][2, 8, 6, 8, 4, 4, 6][8, 6, 2][6, 3, 9, 4][5, 4, 4]defnext_feed():batch = next(batches) encoder_inputs_, _ = helpers.batch(batch) decoder_targets_, _ = helpers.batch( [(sequence) + [EOS] forsequence inbatch] ) decoder_inputs_, _ = helpers.batch( [[EOS] + (sequence) forsequence inbatch] ) return{ encoder_inputs: encoder_inputs_, decoder_inputs: decoder_inputs_, decoder_targets: decoder_targets_, }
给定encoder_inputs [5,6,7],decode_target将为[5,6,7,1],其中1为EOS,decode_inputs为[1,5,6,7] - decode_inputs滞后1步, 将以前的指令作为当前步骤的输入。
loss_track = []max_batches = 3001
batches_in_epoch = 1000
try:
forbatch inrange(max_batches): fd = next_feed() _, l = sess.run([train_op, loss], fd) loss_track.append(l)
ifbatch == 0orbatch % batches_in_epoch == 0: print( 'batch {}'.format(batch)) print( ' minibatch loss: {}'.format(sess.run(loss, fd))) predict_ = sess.run(decoder_prediction, fd) fori, (inp, pred) inenumerate(zip(fd[encoder_inputs].T, predict_.T)): print( ' sample {}:'.format(i + 1)) print( ' input > {}'.format(inp)) print( ' predicted > {}'.format(pred))
ifi >= 2:
breakprint()
exceptKeyboardInterrupt: print( 'training interrupted')
batch 0 minibatch loss: 2.208172082901001 sample 1: input > [9 8 4 0 0 0 0 0] predicted > [3 3 0 8 0 0 0 0 0] sample 2: input > [3 4 3 5 6 0 0 0] predicted > [9 9 8 8 9 9 9 0 0] sample 3: input > [2 2 4 7 5 9 6 3] predicted > [0 9 9 9 4 9 9 9 9]batch 1000 minibatch loss: 0.2542625367641449 sample 1: input > [5 4 9 8 8 0 0 0] predicted > [5 4 9 8 8 1 0 0 0] sample 2: input > [3 9 4 2 3 0 0 0] predicted > [3 9 4 2 3 1 0 0 0] sample 3: input > [2 6 4 4 7 0 0 0] predicted > [2 4 4 4 7 1 0 0 0]batch 2000 minibatch loss: 0.15775370597839355 sample 1: input > [7 7 7 2 3 6 0 0] predicted > [7 7 7 2 3 6 1 0 0] sample 2: input > [8 3 9 9 5 9 0 0] predicted > [8 3 9 9 5 9 1 0 0] sample 3: input > [3 2 9 4 2 6 6 3] predicted > [3 2 9 4 6 6 6 3 1]batch 3000 minibatch loss: 0.1039464920759201 sample 1: input > [8 6 2 3 0 0 0 0] predicted > [8 6 2 3 1 0 0 0 0] sample 2: input > [2 7 9 6 6 5 2 0] predicted > [2 7 9 6 6 5 2 1 0] sample 3: input > [3 3 8 5 4 0 0 0] predicted > [3 3 8 5 4 1 0 0 0]
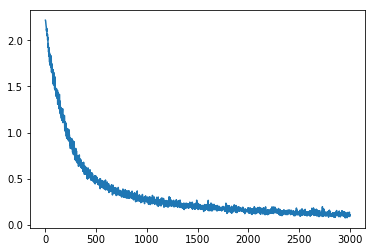
%matplotlib inline importmatplotlib.pyplot aspltplt.plot(loss_track)print( 'loss {:.4f} after {} examples (batch_size={})'.format(loss_track[- 1], len(loss_track)*batch_size, batch_size))
loss 0.1073 after 300100 examples (batch_size=100)
模型的局限性
我们无法控制tf.nn.dynamic_rnn的转换,它在单次扫描中展开。 在没有这种控制的情况下,一些事情是不可能的:
我们无法提供以前生成的指令,而不会退回到Python循环。 这意味着我们无法使用dynamic_rnn解码器进行有效的推断!
我们不能使用Attention,因为Attention条件解码器输入其先前的状态
解决方案是使用tf.nn.raw_rnn而不是tf.nn.dynamic_rnn作为解码器。
- END -
关注者
从1到10000+
我们每天都在进步
相关阅读:
相关推荐: